図1に示すように、電源電圧\(\dot{E}[V]\)、角周波数\(\omega[rad/s]\)の交流電源に、抵抗1個、コイル2個及びスイッチ1個から成る回路が接続されている、抵抗\(R[\Omega]\)であり、2個のコイルは、自己インダクタンスがいずれも\(L[H]\)、相互インダクタンス\(M[H]\)である。また、\(\dot{I_1}\)は電源から流れる電流、\(\dot{I_2}\)はスイッチSが閉じているときスイッチに流れる電流である。なお\(\dot{I_1}\)、\(\dot{I_2}\)はいずれも定常状態の電流である。
スイッチSが開いているときの\(\dot{I_1}\)の大きさ\(\vert \dot{I_1}\vert [A]\)は、\(\vert \dot{E}\vert=E\)とすると、
\[\displaystyle \vert \dot{I_1}\vert=\frac{E}{\sqrt{\fbox{1}}}\]
であり、Sの極間電圧\(\dot{V_{bd}}\)の大きさ\(\vert \dot{V_{bd}} \vert[V]\)は、
\[\displaystyle \vert \dot{V_{bd}}\vert=\frac{E \sqrt{\fbox{2}}}{\sqrt{\fbox{3}}}\]
となる。また、このときで電源からの供給電力\(P_0 [W]\)は、
\[\displaystyle P_0=\frac{E^2 \times \fbox{4}}{\fbox{5}}\]
となる。
次に、図1のa,b,c3端子の相互インダクタンスを含む回路を図2の等価な自己インダクタンス回路に変換することを考える。
図1の回路におけるac間の電圧\(\dot{V_{ac}}\)は、
\[\displaystyle \dot{V_{ac}}=j\omega \times (\fbox{6}) \times \dot{I_1}-j \omega \times (\fbox{7}) \times \dot{I_2}\]
であり、図2の回路におけるac間の電圧\(\dot{V_{ac}}\)は、
\[\displaystyle \dot{V_{ac}}=j\omega L_1 \dot{I_1} +j\omega L_3 (\dot{I_1}-\dot{I_2})となる。\]
となる。等価変換であるので、図1の回路における\(\dot{V_{ac}}\)と図2の回路における\(\dot{V_{ac}}\)とは等しい、したがって、
\(L_1=\fbox{8}[H]\) \(L_3=\fbox{9}[H]\)
となる。また、電圧\(\dot{V_{bc}}\)についても同様に計算すると、
\(L_1=L_2[H]\)となる。
図2においてSが閉じているとき、電源から見た回路の合成インピーダンス\(\dot{Z}\)の大きさ\(\vert \dot{Z}\vert\)は、
\[\displaystyle \vert \dot{Z}\vert=\frac{\omega(L-M) \times \sqrt{\fbox{10}}}{\sqrt{\fbox{11}}}\]
であり、このとき\(\vert \dot{I_1}\vert[A]\)は、
\[\displaystyle \vert \dot{I_1}\vert=\frac{E \times \sqrt{\fbox{12}}}{\omega(L-M) \times \sqrt{\fbox{13}}}\]
\(\vert \dot{I_2}\vert[A]\)は、
\[\displaystyle \vert \dot{I_2}\vert=\frac{E \times \sqrt{\fbox{14}}}{\omega(L-M) \times \sqrt{\fbox{15}}}\]
抵抗Rに流れる電流\(\vert \dot{I_3}\vert[A]\)は、
\[\displaystyle \vert \dot{I_3}\vert =\frac{E}{\sqrt{\fbox{16}}}\]
また、このときの電源からの供給電力\(P[W]\)は、
\[\displaystyle P=\frac{E^2 \times \fbox{17}}{\fbox{18}}\]
となる。
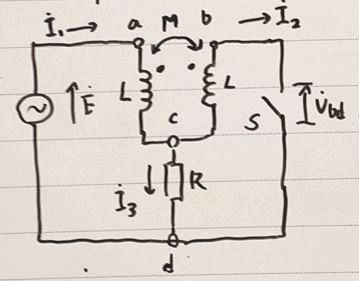
図1
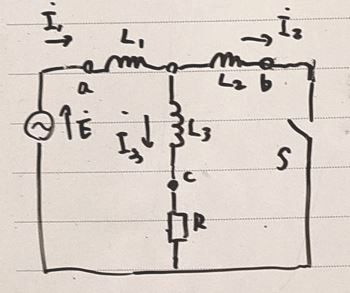
図2


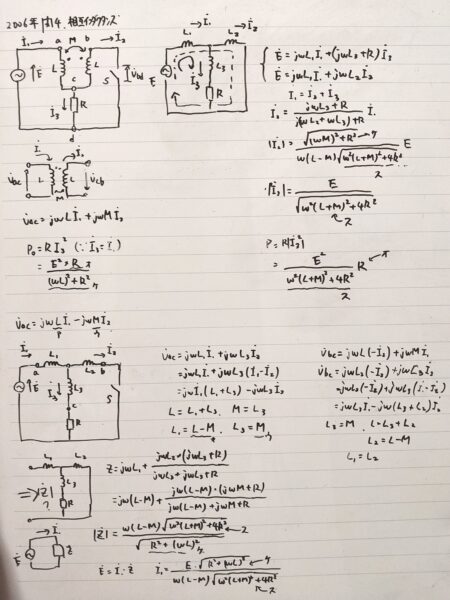


コメント