(2) ある工場の送風設備 (送風機定格出力\(30\)kWにおいて、現状では吐き出しダンパの開度制御
によって風量調節を行っている。 これから、この設備に汎用インバータによる速度制御を導入する
ことで、省エネルギー化を図ることを考える。現状の運用では、1日のうち\(10\)時間は定格風量の\(80\%\)で、\(14\)時間は定格風量の\(50\%\)で運転しており、この設備の更新後も同じ運用を行う。
現状の設備では、送風機の定格動作点での効率 (実際値) が \(80\%\)であり、 電動機 (誘導電動機)の効率は\(85\%\) (動作点によらず一定) である。電動機を三相交流電源に直接接続して定格速度で運転しており、吐き出しダンパ制御によって必要な風量 (\(80\%\)又は\(50\%\))を得ている。この送風設備の風圧-風量特性、風道の送風抵抗曲線及び送風機効率は、それぞれ以下の式で表される。
\[\displaystyle h=1.2n^2 +0.5nq -0.7q^2・・・①\]
\[\displaystyle r=q^2・・・②\]
\[\displaystyle \eta =2.0(\frac{q}{n})-(\frac{q}{n})^2・・・③\]
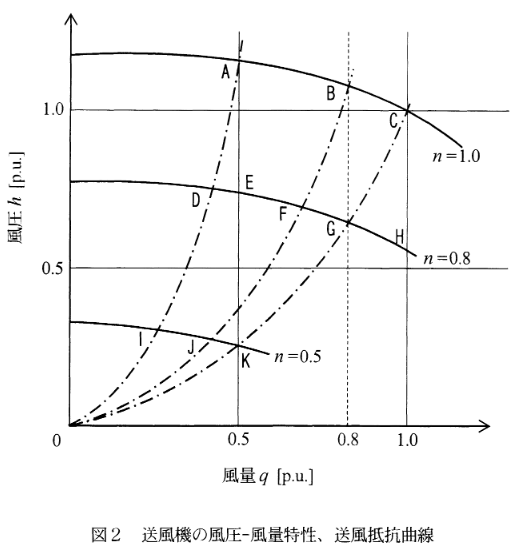
ここで、\(h\)は風圧、\(n\)は回転速度、\(q\)は風量、\(r\) は送風抵抗、\(\eta\)は送風機効率であり、いずれも送風機定格点での値で正規化した (p.u.で表した)ものである。 図2に、1式及び2式で与えられる送風機の風圧-風量特性、及び送風抵抗曲線を表す。
1)現状の設備における1日の消費電力量について考える。吐き出しダンパを開度制御して定格風量の\(80\%\)で運転する \(10\) 時間においては、図2中の動作点 \(6\) で運転している。このとき、 \(h= 1.15\) [p.u]、\(\eta=\fbox{A}×10^{-1} \)[p.u.]、送風機軸入力\(p=0.960 \)[p.u.]となる。また、定格風量の\(50\%\)で運転する \(14\)時間においては、図中の動作点このとき、\(h=\fbox{B}\)[p.u]、\(\eta = 0.75\) [p.u.] 送風機軸入力\(p=\fbox{C}×10^{-1}\)[p.u]となる。送風機の定格出力が\(30\)kW、 送風機効率が\(80\%\)、電動機効率が\(85\%\) なので、風量\(80\%\)の\(10\) 時間における消費電力量は\(424\) [kWh] となり、風量 \(50\%\)の \(14\) 時間における消費電力量は\(\fbox{D}\)[kWh] となる。
2) 汎用インバータによる速度制御を導入した場合の消費電力量について考える。
電動機は更新せずに、汎用インバータ(インバータ効率\(95\%\)) による速度制御を導入し、吐き出しダンパは全開して、 速度制御によって必要な風量 (\(80\%\) 又は \(50\%\)) を得ることとする。なお、速度制御の導入後も ①~③式は成り立つものとする。
定格風量の\(80\%\)で運転する \(10\)時間においては、図中の動作点Gで運転している。 このとき、\(h=\fbox{E}×10^{-1}\)[p.u]、\(\eta =1.0 \)[p.u.]、 送風機軸入力\(p=\fbox{F}×10^{-1} \)[p.u.] となる。また、定格出力の\(50\%\)で運転する\(14\)時間においては、図中の動作点\(\fbox{8}\)で運転しており、\(p=\fbox{G}×10^{-1}\)[p.u]となる。
設備の更新前と同様に、 送風機の定格出力が\(30\)kWで、送風機効率が\(80\%\)、 電動機効率が\(85\%\)として、更にインバータ効率が\(95\%\)なので、 1日の消費電力量は\(\fbox{H}\)[kWh]となる。
以上を踏まえると、汎用インバータによる速度制御を導入することにより、 1日当たりの消費電力量は、現状のおよそ3分の1まで低減されることが分かる。
解説動画




コメント