
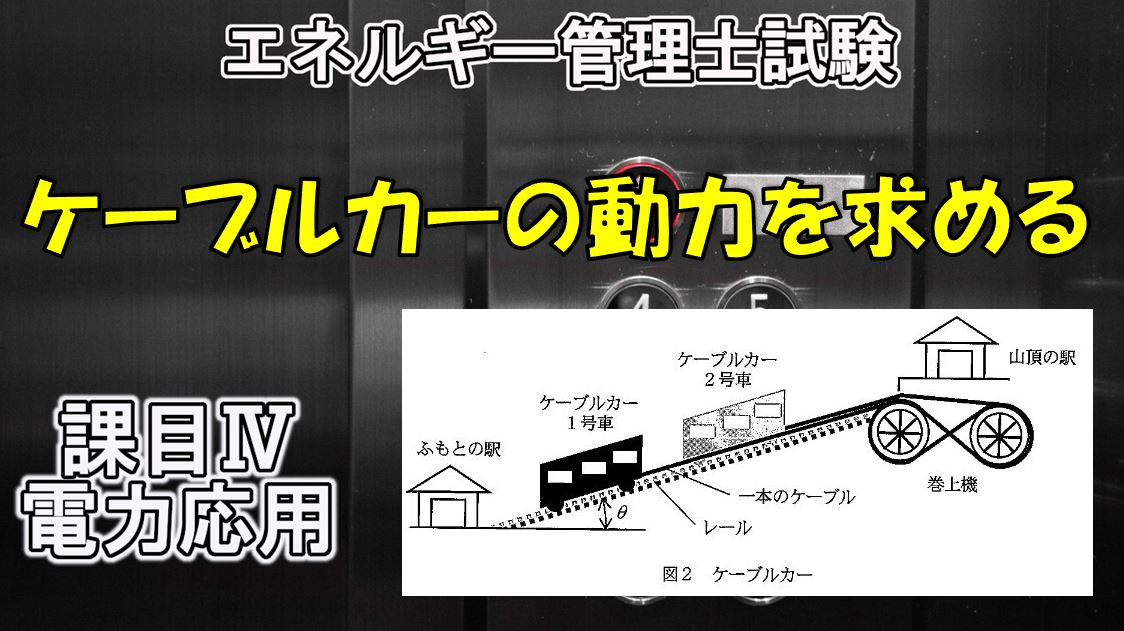
(2)図2に示すような、勾配角度\(\theta\)の線路を運行する2台のつるべ式(交走式)ケーブルカーの動力について考える。
ケーブルカーは車両に動力を持たず、車両につないだケーブルを山頂にある巻上機で引っ張り上げて走行させている。
つるべ式ケーブルカーでは、一本のケーブルの両側に車両をつなぎ、登り側車両と下り側車両を同時に走行させる仕組みとなっており、国内のほとんどのケーブルカー ではつるべ式を採用している。
ここでは、ケーブルの巻上機に用いられる電動機に関して、運行形態ごとの電動機の所要出力を求める。
ここで、ケーブルカーの運行速度は\(180 m/min\)、一車両当たりの車両質量は\(5000kg\)、乗客の最大搭乗質量(満員時)は\(1600kg\)、巻上機全体の機械効率は\(70\%\)とし、ケーブル荷重など記載のない条件は無視する。
なお、線路勾配角度\(\theta\)は\(30度\)、斜面における走行抵抗は、重力の加速度\(g\)に関して \(10・g \times 10^{-3} \times \cos{\theta}[N/kg]\)であり、重力の加速度\(g\)は\(9.8 m/s\)とする。
1) ケーブルの片側だけに1号車の車両をつなぎ、登りの一車両だけ運行する状況を考える。
電動機が最大出力を必要とするのは、満員の乗客で登坂する場合である。
この場合、斜面に沿って\(180m/min\)で走行するとき、走行抵抗に打ち勝つために要する動力は、斜面方向に働く力と登坂速度を乗じて\(\fbox{A}[kW]\)である。
また、車両と乗客の全質量を斜面に沿って\(180m/min\)で引っ張り上げるのに要する、単位時間当たりの位置エネルギーの増加分に相当する動力は、\(\fbox{B}[kW]\)となる。
そして、それらの動力を合算し、巻上機全体の機械効率を考慮すると、このときに電動機が要求される出力は\(\fbox{C}[kW]\)となる。
2) 残りの片側に2号車をつないでケーブルの両側に車両がある状態とし、つるべ式で登り側車両と下り側車両を同時に運行させる状況を考える。
電動機が最大出力を必要とするのは、登り側車両が満員で下り側車両には乗客がいない場合である。
この場合、各車両が走行抵抗に打ち勝つために要する動力は、満員の登り側車両分と乗客のいない下り側車両分を合わせて\(\fbox{D}[kW]\)である。
その一方で、車両の移動に関しては、登り側と下り側の車両質量が等しいことから、車両の上昇と下降に要する動力は相殺する。
したがって、乗客の全重量だけを斜面に沿って引っ張り上げるのに要する動力を考慮すればよい。
乗客がいるのは登り側だけなので、そのために要する動力は\(\fbox{E}[kW]\)となる。
よって、それらの動力を合算し、巻上機全体の機械効率を考慮すると、このときに電動機が要求される出力は\(\fbox{F}[kW]\)となる。
以上の結果から、つるべ式によるケーブルカーの運行が効率的であることが分かる。




コメント