単相2線式と単相3線式の線路損失について考える。なお、計算に当たっては、負荷力率は100%、負荷電流は一定とし、線路抵抗以外のインピーダンスは無視するものとする。
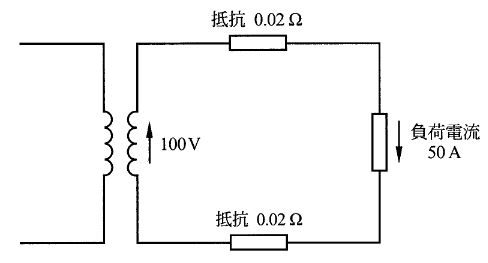
1)単相2線式は、2線で電源を供給する方式であり、図1に示すように、電線の抵抗が\(0.02\Omega\)の\(100V\)単相2線式配電線路において、\(50A\)の負荷が接続されている場合、線路損失は\(\fbox{A}[W]\)である。
2)単相3線式は、変圧器2次側の中性点を接地し、単相2線式に中性線1線を加えて、合計3線で電源供給する方式である。図2(a)の\(100/200V\)単相3線式配電線路において、電圧線及び中性線の抵抗が、それぞれ\(0.02\Omega\)であり、\(30A\)及び\(20A\)の二つの負荷が接続され散るとき、中性線に流れる電流は\(\fbox{B}[A]\)であるから、3線合計の線路損失は\(\fbox{C}[W]\)である。

この配電線路において、図2(b)のようにバランサを接続した場合、配電線路に流れる電流の\(\fbox{7}\)が改善され、バランサがない場合に比べ、線路損失は\(\fbox{D}[W]\)減少する。また、図1の単相2線式と比較すると、線路損失は\(\fbox{8}\)倍となる。
図1に示すような、負荷A、負荷Bに電力を供給する単相3線式配電回路があり、各線路の抵抗は等しく\(R\)である。このときの線路全体の電力損失を求める、ただし、すべての負荷の力率は100%とする。
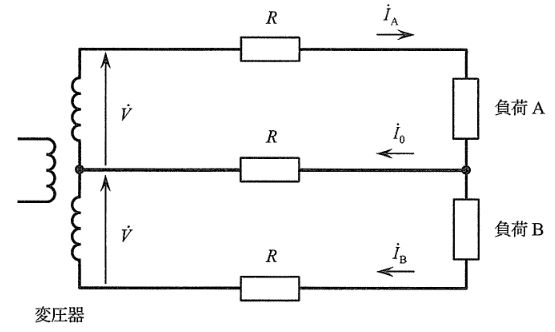
ここで、線路電流\(\dot{I}_A\)の大きさを\(I_A\)、線路電流\(\dot{I}_B\)の大きさを\(I_B\)、線路電流の\(\dot{I}_0\)のおおきさを\(I_0\)とし、\(I_A\)と\(I_B\)の和の\(\frac{1}{2}\)を\(I\)、\(\frac{I_0}{I_A+I_B}\)を\(\alpha\)としたとき、\(I_A\)、\(I_B\)及び\(I_0\)の関係は、次の式④及び⑤であらわされる。
\[I_A + I_B = 2I・・・④\]
\[I_0=I_A – I_B = \alpha(I_A+I_B)=2 \alpha I ・・・⑤\]
式④及び式⑤から、線路全体の電力損失\(W\)は\(I\)、\(\alpha\)及び\(R\)を用いて、次の式⑥で表される。
\[W=\fbox{8}\]
(6)単相三線式配電線において平衡分流(両電圧線の線路電流の和の\(\frac{1}{2}\))を\(I\)とし、電流不平衡率=(中性線電流/両電圧線の線路電流の和)を\(\alpha\)としたとき、この線路全体の電力損失は\(\fbox{1}\)である。
ただし、両電圧線の抵抗は等しく\(R\)とし、中性線の抵抗は電圧線の抵抗の\(\frac{1}{2}\)とし、すべての負荷の力率は100%とする。




コメント