見にくい場合は設定でHD画質にすると多少見やすくなります。
2011年 問5 自動制御(類似問題出題年 多数)
1)図1に示すブロック線図について考える。ここで、\(T\)及び\(K\)は正の有限な定数である。
①ブロック\(A\)のゲイン定数は\(\fbox{1}\)であり、ブロック\(B\)は伝達関数は\(\fbox{2}\)要素と呼ばれる形である。
②\(r\)から\(y\)への伝達関数は\(\fbox{3}\)となる。
③\(r\)から\(\omega\)の伝達関数のステップ応答を早くするためには、\(\fbox{4}\)すればよい。
④\(r\)に大きさ1のステップ波形を加えて、十分な時間が経過したときの\(\omega\)の値は\(\fbox{5}\)であり、
\(y\)の値は\(\fbox{6}\)である。
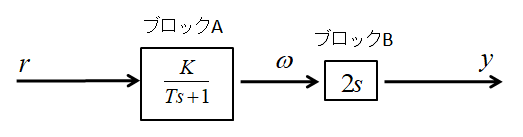
図1

2)図2に示すブロック線図について考える。ここで、\(T\)、\(K\)及び\(K_c\)はある正の有限な定数である。
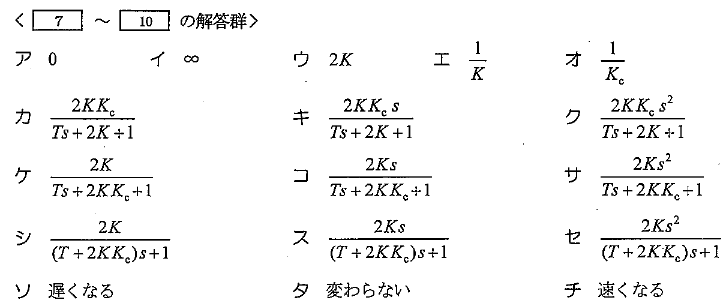
①\(\acute{r}\)から\(y\)への伝達関数は\(\fbox{ 7 }\)
②\(\acute{r}\)に大きさ1のステップ波形を加えた時の\(y\)のラプラス変換は\(\fbox{8}\)となり、この応答において、
十分な時間が経過したときの\(y\)の値は\(\fbox{9}\)である。
③\(\acute{r}\)から\(y\)の伝達関数のステップ応答の速さは、\(K_c\)を大きくすると\(\fbox{10}\)。
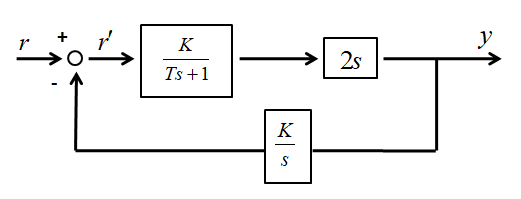
図2




コメント