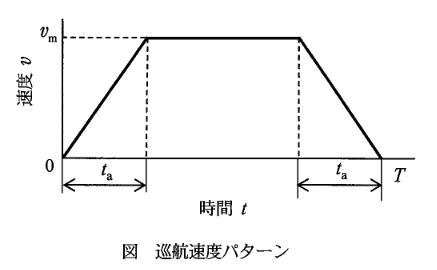
(1)電気自動車の消費エネルギーを考える。簡略化のため、巡航速度を\(v_m[m/s]\)一定とし、図のような速度パターンで水平な道路を直進するものとする。
駆動力を\(f_M[N]\)、抗力を\(f_L[N]\)、速度を\(v[m/s]\)とすると、次の運動方程式が成り立つ。
\[\displaystyle m_e \frac{dv}{dt}=f_M – f_L・・・①\]
ここで、\(m_e[kg]\)は等価的な質量であり乗員を含む車両全体の質量\(m[kg]\)、電動機や車輪など回転系全体の慣性モーメント(車輪軸換算)\(J[kg・m^2]\)、及び車輪の半径\(r[m]\)を用いて次式で与えられる。
\[\displaystyle m_e=m + \frac{J}{r^2}・・・②\]
一方、抗力は転がり抵抗による抗力と空気抵抗による抗力の和として次式で与えられる。
\[\displaystyle f_L = C_{rr} mg + \frac{1}{2} \rho v^2 C_d A・・・③\]
ここで、タイヤの・・・
(中略:各種抵抗値についての最近の自動車についての説明)
さて、図のように\(0s\)から\(T[s]\)までの走行区間において、走行開始から\(t_a\)秒間を加速区間、停止前の最後の\(t_a\)秒間を減速区間とし、両者の間の区間を等速区間として走行したとき、走行開始から停止するまでの走行距離\(X[m]\)と走行時間\(T\)の間には次の関係が成り立つ。
\[\displaystyle X = \int_0^T v dt = v_m \times \fbox{1}・・・④\]
簡略化のため、電力変換器や電動機などの電気系での損失を無視すると、電源であるバッテリーから走行期間中に供給されるエネルギー\(E_0[J]\)は次式で計算される。
\[\displaystyle E_0 = \int_0^T f_M v dt = \int_0^T (m_e \frac{dv}{dt} + f_L)v dt\]
\[\displaystyle = \int_0^{0+t_a} (m_e \frac{dv}{dt}) v dt+ \int_{T-t_a}^T (m_e \frac{dv}{dt})v dt + \int_0^T f_L v dt\]
\[\displaystyle \frac{1}{2}m_e {v_m}^2 – \frac{1}{2}m_e {v_m}^2 + \int_0^T f_L v dt =\int_0^T f_L v dt・・・⑤\]
このように加速区間では運動エネルギー分が供給されるが、減速区間でかいせいされるので、走行区間全体でみると抗力に相当するエネルギーのみが供給される。式⑤の結果に式③を代入して、図の速度パターンで運転する場合について区間を分けて計算すると次の結果を得る。
\[\displaystyle \int_0^{0+t_a} f_L v dt =\int_{T-t_a}^T f_L v dt =(\fbox{2} \times C_{rr}m g v_m + \fbox{3} \times \rho C_d A {v_m}^3)t_a・・・⑥\]
\[\displaystyle \int_{0+t_a}^{T-t_a} f_L v dt = (C_{rr}mgv_m + \frac{1}{2}\rho C_d A {v_m}^3)(T-2t_a)・・・⑦\]
従って、式④の関係を考慮すると、\(E_0\)は次式で表される。
\[\displaystyle E_0= \int_0^T f_L v dt = C_{rr}mgv_m \times \fbox{4} + (\frac{1}{2}\rho C_d A {v_m}^2)\times \fbox{5}・・・⑧\]
ここまでの検討では電気系の損失を零と仮定したが、実際には無視できない。運動エネルギーは電力変換器や電動機を通して行き来するため、これらの高効率化が重要である。


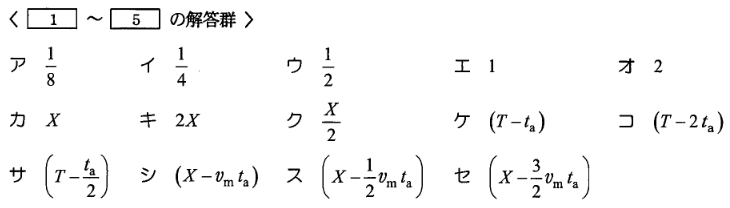


コメント