2021年課目４問１１（２）運搬用電気車両のモデルを使ったエネルギー

2021年課目４問１１（２）運搬用電気車両のモデルを使ったエネルギー

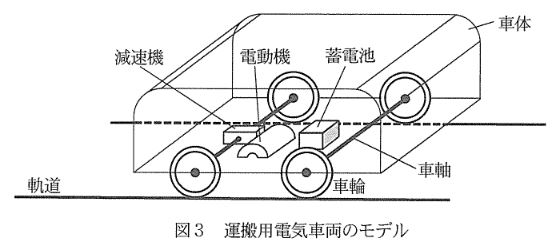
図３は水平な直線器上場を移動する運搬用電気車両のモデルを表す。この車両は、四つの車輪が二つの車軸で連結され、うち一つの車軸には減速機が備えられている。減速機には電動機が接続されており、蓄電池から電動機へ電力が供給されている。

減速機の減速比を１：ｎとするとき、車軸並びに車輪の回転速度\(\omega[rad/s]\)は、電動機の出力軸の回転角速度\(\omega_M[rad/s]\)に関して\(\frac{1}{n}\)と表される。電動機への供給される電流を\(I[A]\)、電動機のトルク定数を\(K[N・m/A]\)とするとき、電動機の入力トルクは\(K・I[N・m]\)と表される。

このモデルにおいて、全ての構成要素の合算質量を車両質量\(M[kg]\)とし、回転運動するすべての要素（電動機の回転子及び出力軸、減速機の構成要素、車輪など）全体の慣性モーメント（車軸換算）を\(J[kg・m^2]\)として考える。

また、車両の走行時に発生する摩擦として、電動機及び減速機内部で生じる粘性摩擦を考慮し、粘性摩擦トルク\(\tau[N・m]\)を考える。このとき、\(\tau\)は車軸の回転角速度\(\omega\)に比例するものとみなして、\(\tau=D\omega\)と表す。ここで係数\(D\)は正の定数とする。車輪と起動の接触点において滑りは生じないものとし、前記の粘性摩擦以外の摩擦や抵抗は無視する。

この車両に関して、図４の電流パターンを供給して運転し、図５の車軸の回転角速度パターンで走行させた場合について考える。

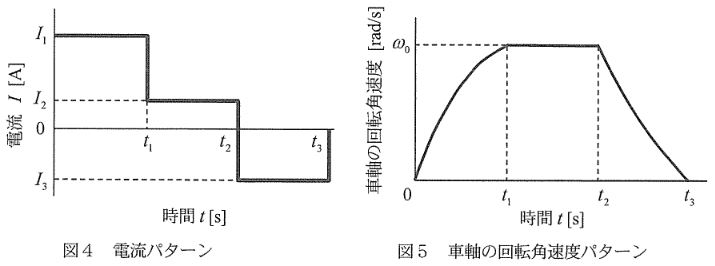
１）走行時にこの車両の持つ運動エネルギーについて、直線運動と回転運動に分けて考える。車両が一定速度\(v_0[m/s]\)で走行しているとき、質量\(M\)の車両全体が持つ直線運動による運動エネルギーは\(\fbox{10}[J]\)である。また、車輪の半径を\(a[m]\)とすると、このときの車軸の回転角速度は\(\fbox{11}[rad/s]\)であるから、回転運動する要素が持つ回転運動による運動エネルギーは\(\fbox{12}[J]\)である。

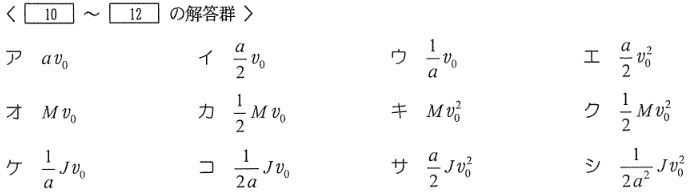
２）この車両について、車軸に関する運動方程式は、回転角加速度\(\dot{\omega}[rad/s^2]\)を用いて次式で表される。

\[\displaystyle (J+a^2M)\dot{\omega}=nKI-D\omega・・・①\]

ここで、この車両を図４に示す電流パターンに従い、車両の初速を\(0[m/s]\)として、\(0 \leq t \leq t_1\)で一定電流\(I_1[A]\)を電動機へ与えるとき、式①に基づけば、この間の車軸の回転角速度は、自然対数の底\(e\)を用いて次式で求められる。

\[\displaystyle \omega=\frac{nK}{D}I_1\{1-e^{-(\frac{D}{J+a^2 M}t)}\}・・・②\]

式①と式②を踏まえると、\(t=0\)における車軸の回転角加速度は\(\fbox{13}[rad/s^2]\)である。また、\(t_1 \leq t \leq t_2\)で車軸の回転角速度\(\omega_0[rad/s]\)で等速走行するので、その間に供給される電流\(I_2[A]\)は式\(I_2=\fbox{14}[A]\)と求めることができる。

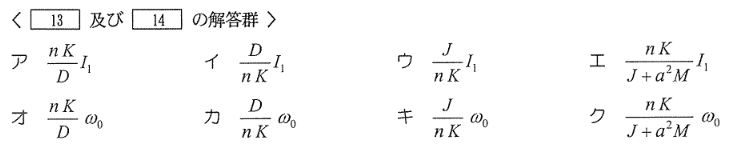
３）\(t_2 \leq t \leq t_3\)の減速時に、負の電流\(I_3\)を与えて車両を減速・停止させるとき、加速に要する時間\(t_1[s]\)と減速に要する時間\((t_3-t_2)\)が等しいとすると、電流\(I_3\)の絶対値は電流\(I_1\)の絶対値より小さい値になる。\(t_2 \leq t \leq t_3\)の回転角速度を１次関数として近似するならば、式①の運動方程式は次式に近似できる。

\[\displaystyle (J+a^2M)\dot{\omega}=n\acute{K}I_3・・・③\]

ここで、\(\acute{K}\)は正の定数とする。式③を踏まえると、\(t_2 \leq t \leq t_3\)の回転角速度を近似した１次関数は次式で表される。

\[\displaystyle \omega=\fbox{15}・・・④\]

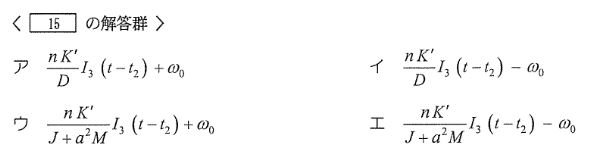
４）図５の速度パターンにおいて、\(t=t_2[s]\)の時点で車両が持つすべての運動エネルギーのうちの２０％が、\(t=t_3[s]\)で静止するまでに摩擦によって失われ、残りの８０％が蓄電池へ回生されたとする。車体全質量\(M\)を\(3000kg\)、車軸から見た総合的な慣性モーメント\(J\)を\(250kg・m^2\)、車輪半径\(a\)を\(0.5m\)、\(t=t_2\)の時点での車両速度\(v_0\)を\(6m/s\)とするならば、蓄電池へ回生された電力量は\(\fbox{16}[W・h]\)になる。