電験3種は5択式であり、電験2種の一次試験は15択の選択肢から適当なものを選ぶ形式です。
ただし、空欄に対してある程度どれが対象とする選択肢なのかはある程度問題から絞れることもあります。
本番では思ったように問題が解けず、最終的にかなり勘に頼ったところがありましたが、それでも少なからず正答に近づけた上で勘に頼ります。
今回はその方法である”次元解析”を紹介したいと思います。
気が付かずにやっている人も多いのではないかと思います。
次元解析のやりかた
わかりやすくするために理論科目から引用してきます。
他の科目でもできることがありますが、一番効果を発揮するのは記号問題が多い理論科目かなと思います。
今回はより効果を発揮する2種一次試験を例に出していますが、3種の計算問題でも適用できる場合があります。
令和元年度 電験2種 一次試験の理論科目問4
問題文はあまり関係が無いので今回は出題された問いから、次元解析のポイントとなるところのみを抽出します。
問題文の全文は電気技術者センターより閲覧することができます。
https://www.shiken.or.jp/answer/pdf/327/file_nm01/S1-R.PDF
ここでは問題文一部のみ掲載しており、この一部から次元解析を用いて選択肢を絞っていきましょう。

(1)はこの式。
$$\dot{Z_0}=\frac{1}{(\quad(1)\quad)}$$
(1)に入るものは左辺を見るとインピーダンスなので単位は\([\Omega]\)です。
右辺も同様に\([\Omega]\)が入るはずなので、分母が1であることから、(1)は\(\frac{1}{\Omega}\)が入ることがわかります。
回答群を見ると。
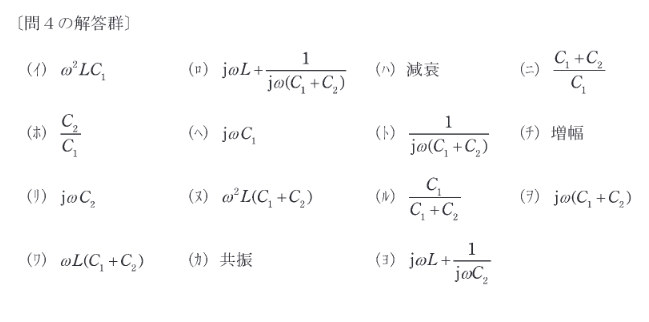
一見皆似たような選択肢に見えますが、この中で単位オームの逆数\([/\Omega]\)になっているのは。

この3つが当たります。リアクタンス\(\dot{X_c}=\frac{1}{j \omega C} [\Omega]\)
迷ったらこの3つから選べばそれだけで確率33.3%で当たります。
次に(2)の式を見ていきます。
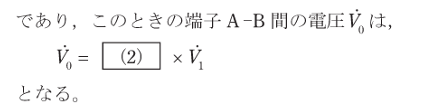
$$\dot{V_0}=(\quad(2)\quad) \times \dot{V_1}$$
この場合左辺と見えている右辺がどちらも単位がボルトなので、(2)に入るものは単位としては存在しない係数のようなものが入ると予想されます。
また解答群を見ていると。

この3つは単位がありません。この中に正解がある確率が高いです。
続いて(3)にいきます。

$$\dot{V_2}=\dot{I} \times \dot{Z}=\frac{(\quad(2)\quad) \times \dot{V_1}}{(\quad(3)\quad) + \dot{Z}} \times \dot{Z}$$
(3)に入るものは\(\dot{Z}\)と足し算できるものであり、足し算引き算ができるものは同じ単位を持つものである必要があります。
ですので(3)はインピーダンスである必要があるため、

この3つが該当します。

続く(4)は\(L,C_1,C_2\quad (4)=1\)の関係とあります。
第一候補はすべての記号を使用している物になりますが、次元解析としては、右辺が1になるため、左辺の単位は無い。と考えると。

この3つが該当します。
ただ、この(4)については(3)の項が零になる。と問題文中にあるため、例外として
(3)=0であるとして、(3)の3つの候補=0から式変形できるものに限ると(ヌ)に限定されます。

最後は日本語が入るだろう。と見れば、

この3つが該当します。
このように次元だけで答えをある程度絞ることができるため、解けなかった場合にはこれらから類推して選択肢を絞るのも一つの手です。
今回はたまたま(4)が限定できましたので、2問は正解できるかなと思いますが、まったく分からなくても、1問程度は確率で拾えることになります。
最後の最後はその1~2問が明暗を分ける場合もあるため少しでも可能性を求めて諦めずに解析してマークを埋めましょう。
がんばってください!




コメント