リニアモータで推進される\(1000kg\)の台車が、平坦な線路上を、図1に示すように加減速することを考える。完全停止から速度\(10m/s\)まで一定の加速度で加速していき、出発して時間\(20s\)後に惰行運転となった。さらに、出発して\(100s\)後に回生制動を行って一定の減速度(負方向の加速度)で減速し、出発して\(120s\)後に完全停止した、ここで、走行抵抗は速度にかかわらず一定とする。また、回生制動によるエネルギー回収率は100%とする。
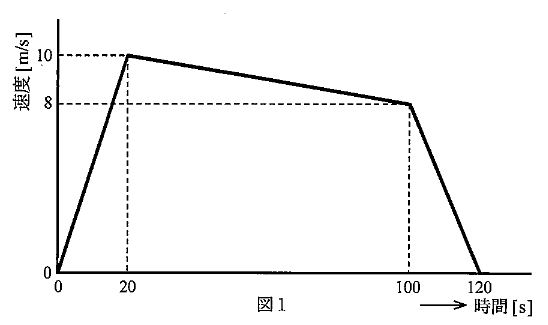
1)台車の走行距離は\(\fbox{A}[m]\)である。
2)出発後\(20s\)から\(100s\)までの惰行運転中に、走行抵抗により台車の速度が\(10m/s\)から\(8m/s\)まで減速している。この間の減速度は\(\fbox{B}\times 10^{-2}[m/s^2]\)である。
3)台車は出発後\(20s\)で\(10m/s\)まで加速される、この間にリニアモータは、加速のための推力と走行抵抗負荷に打ち勝つ推力の合計を発生しなくてはならないため、その推力値は\(\fbox{C}[N]\)になる。
4)出発してから停止するまでの走行抵抗による損失エネルギーは\(\fbox{D}[kJ]\)である。
5)回生制動により回収したエネルギーは\(\fbox{E}[kJ]\)である。




コメント