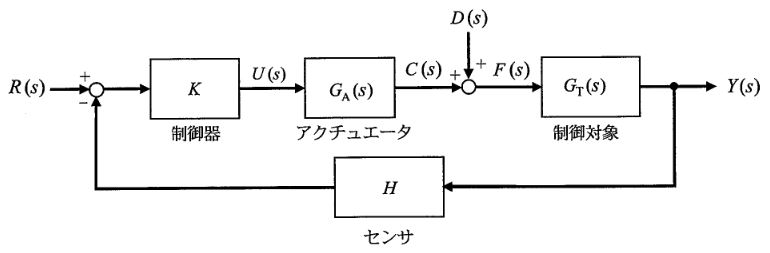
図1に示すようなフィードバック制御系を考える。ここで、\(t\)を時間、参照値を\(r(t)\)、制御器出力を\(u(t)\)、操作量を\(c(t)\)、外乱を\(d(t)\)、制御対象への入力を\(f(t)\)、制御量を\(y(t)\)とし、\(R(s)\)は\(r(t)\)を、\(U(s)\)は\(u(t)\)を、\(C(s)\)は\(c(t)\)を、\(D(s)\)は\(d(t)\)を、\(F(s)\)は\(f(t)\)を、\(Y(s)\)は\(y(t)\)を、をそれぞれラプラス変換したものとする。また、\(K\)と\(H\)は定数であり、\(K=100\)、\(H=0.2\)とする。ここで、すべての物理量は無次元で表現する。
1)いま、アクチュエータの伝達関数\(G_A (s)\)が次の式で与えられるとする。
\[\displaystyle G_A (s)=\frac{b}{s+a}\]
この伝達関数の単位ステップ応答が\(100(1-e^{-10t})\)であるとすると、\(a\)は\(\fbox{1}\)、\(b\)は\(\fbox{2}\)である。
2)次に制御対象の伝達関数\(G_T (s)\)について考える。\(G_T (s)\)が次の時間領域関数のラプラス変換したもので表されるとする。
\(G_T (s)=\fbox{3}\)
ここで、\(M=1000\)とすると、伝達関数\(G_T (s)\)は次のように表される。
3)ここで、外乱を\(0\)として\(R(s)\)から\(Y(s)\)までの伝達関数を求めると、\(\fbox{4}\)となる。
4)外乱が\(d(t)=1\)のときに、参照値\(r(t)=A\)を与えた。十分に時間が経過した後に、制御量\(y(t)\)が\(20\)となった。このとき\(A\)の値に最も近いのは\(\fbox{5}\)である。
(2)伝達関数で表現される線形システムの極と応答について考える。
1)もし、すべての極が\(\fbox{6}\)に存在するとき、そのシステムは安定である。
2)次に極が1)と同じ条件であり、制御系設計により、極を移動することができる状況を考える。
ここで、二次遅れ系で極が共役複素根のとき、極の位置を原点に近づけると、システムの応答は\(\fbox{7}\)。一方、極の位置を垂直に実軸に近づけると、システムのステップ応答のオーバーシュートは\(\fbox{8}\)。





コメント