2012年 問4 三相平衡負荷と単相負荷の並列接続(難しいがこれが解ければ大丈夫)
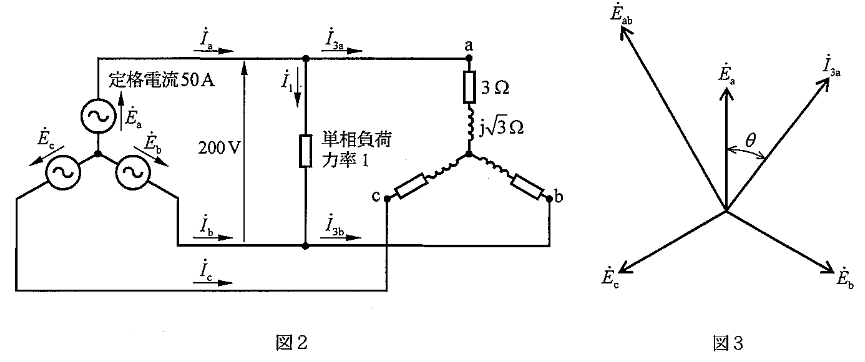
図2に示すように、相電圧\(\dot{E_a}[V]\)、\(\dot{E_b}[V]\)、\(\dot{E_c}[V]\)の対称三相交流電源に、抵抗\(3\Omega\)と
リアクタンス\(\sqrt{3}\Omega\)を直列に接続したものを\(Y\)結線した平衡三相負荷が接続されている。
この電源の線間電圧は\(200V\)、定格電流は\(50A\)である。
電源の定格電流を超えない範囲で、a-b間に力率1の単相負荷を接続する場合の許容容量を求める過程を考える。
ここで、相回転はa-b-cの順とする。なお、図2に示されているインピーダンス以外のインピーダンスは無視するものとする。
1)この回路において、三相負荷の各相のインピーダンスの大きさを\(\dot{Z_3}[\Omega]\)とすると、
\[Z_3=\fbox{7}[\Omega]\]
であることから、三相負荷のa相の電流\(\dot{I_{3a}}[A]\)の大きさ\(I_{3a}[A]\)は、
\[I_3a=\fbox{8}[A]\]
となる。
2)この回路において、\(\dot{I_{3a}}\)と\(\dot{E_a}\)の位相関係は図3のようになり、\(\dot{I_{3a}}[A]\)は\(\dot{E_a}\)に対して位相が、角度\(\fbox{9}\)の\(\fbox{10}\)である。
また、\(\dot{I_{3b}}\)と\(\dot{E_b}\)の関係も同様である。
3)次に単相負荷の電流\(\dot{I_1}[A]\)についてみると\(\dot{I_1}\)の大きさ\(I_1[A]\)は\(\dot{E_a}\)と\(\dot{E_b}\)の差\(\dot{E_{ab}}[V]\)で決まる。
位相に注目すると、\(\dot{I_1}\)は\(\dot{E_a}\)に対して位相が、角度\(\fbox{11}\)の\(\fbox{12}\)となる。
すなわち、\(\dot{I_{3a}}\)と\(\dot{I_1}\)は位相差が\(\fbox{13}\)の関係になる。
また、\(-\dot{I_1}\)は\(\dot{E_b}\)に対して位相が、角度\(\fbox{14}\)の\(\fbox{15}\)となり、\(\dot{I_{3b}}\)との位相差は\(\fbox{16}\)である。
4)これらの関係から、電源からの、a相の電流\(\dot{I_a}[A]\)の大きさを\(I_a[A]\)、b相の電流\(\dot{I_b}[A]\)の大きさを\(I_b[A]\)とすると、
\(I_a[A]\)は\(I_b[A]\)より\(\fbox{17}\)。電源の定格電流50Aを超えないようにするには、\(I_a\)、\(I_b\)、\(I_c\)、のうち電流\(\fbox{18}\)で単相負荷の
大きさが制限されることになる。
したがって、単相負荷電流の最大値\(I_{1max}[A]\)は
\[I_{1max}=\fbox{19}[A]\]
であり、接続できる単相負荷の最大許容容量\(P_{1max}[kW]\)は、
\[P_{1max}=\fbox{20}[kW]\]
となる。





コメント