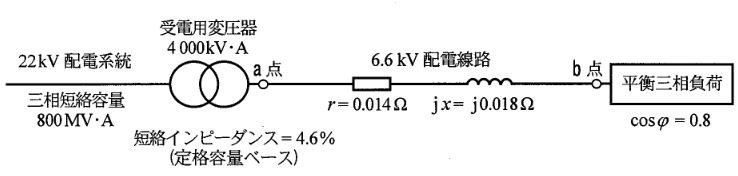
図は、ある工場の配電系統を示したものである。\(22kV\)配電系統に、\(22kV/6.6kV\)の受電用変圧器が接続され、\(6.6kV\)配電線路を介して平衡三相負荷が接続されている。\(22kV\) 配電系統の三相短絡容量は\(800 MV・A\)であり、受電用変圧器は、定格容量が\(4000kV・A\)、定格容量ベースの短絡インピーダンスが\(4.6\%\)である。ここで、\(6.6kV\)配電線路の1相当たりの抵抗\(r\)が\(0.014\Omega\)、1相当たりのリアクタンス\(x\)が\(0.018\Omega\)であり、その他のインピーダンスは無視するものとする。
\(6.6kV\)配電線路には、力率\(\cos{\phi}\)のが\(0.8\)(遅れ)の平衡三相負荷が接続されており、1相当たりの線路電流\(I\)は\(120A\)とする。
1) 配電線路のa~b点間における電圧降下及び電力損失を求める。
線間電圧の電圧降下\(\Delta V [V]\) は、a~b 点間の抵抗\(r\)及びリアクタンス\(x\)を用いて、次の簡略式から求められる。ここで、簡単のために、受電用変圧器二次側の a 点から負荷側を見た力率は、負荷の力率\(cos{\phi}\)と同じとする。
\[\displaystyle \Delta V = \sqrt{3}I(r \cos{\phi} + x\sin{\phi}) [V]\]
これに数値を代入すると次のようになる。
\(\Delta V =\fbox{1}V\)
また、三相分の電力損失\(P [W]\) は、記号を用いて表すと次式となる。
\(P_L=\fbox{2}[W]\)
これに数値を代入すると次のようになる。
\(P_L=\fbox{3} [W]\)
2) 短絡容量や短絡電流を求める際には、機器や線路の短絡容量や百分率インピーダンスを、統一した基準容量に換算して用いると計算が容易になる。
まず、基準容量を\(P[kV・A]\)とし、短絡インピーダンスを基準容量ベースの百分率インピーダンス\(\%Z_s[\%]\)で表すと、短絡容量\(P_s[kV・A]\)は次式で示される。
\[\displaystyle P_s = P \times \frac{100}{\%Z_s}[kV・A] ・・・①\]
次に、\(22kV\) 配電系統、受電用変圧器及び\(6.6kV\)配電線路について、基準容量\(P\)を\(1000kV・A\)としたときの百分率インピーダンスを求める。
\(22kV\)配電系統の百分率インピーダンス\(\%Z\)は、①式より次の値となる。
\[\displaystyle \%Z_s = \fbox{4}[\%]\]
受電用変圧器の百分率インピーダンス\(\%Z_r[\%]\)は、短絡インピーダンスを用いて計算すると次の値となる。
\[\displaystyle \%Z_T = \fbox{5}[\%]\]
\(6.6 kV\)配電線路の百分率抵抗\(\%r [\%]\)は、定格電圧を\(V_r [kV]\)、抵抗を\(r [\Omega]\)とすると次式で示される。
\[\displaystyle \%r = \frac{r \times P}{\fbox{6} \times 10^3} \times 100[\%]・・・②\]
\(6.6 kV\) 配電線路の百分率リアクタンス\(\%x[\%]\)は、リアクタンス\(x[\Omega]\)を用いて②式と同様に求められ、次の値となる。
\[\displaystyle \%x = \fbox{7}[\%]\]

3)次に、短絡電流を計算する。
基準容量\(P\)を\(1000kV・A\)として、\(6.6kV\)配電線路の a 点から電源側を見た基準容量ベースの百分率インピーダンス\(\%Z_a[\%]\)は、\(\%Z_s\)及び\(\%Z_n\)を用いて次式で示される。ここで、簡単のために、\(\%Z_s\)及び\(\%Z_T\)はすべてリアクタンス分のみであるとし、また、短絡時、負荷側から a点 への電流の供給はないものとする。
\[\displaystyle \%Z_a = \fbox{8}[\%]\]
ここで、\(\%Z_a\)の値が\(1.28\%\)であるとして、a点の短絡容量\(P_a[MV・A]\)を算出すると、次の値となる。
\[\displaystyle P_a=\fbox{9}[MV・A]\]
したがって、a 点の三相短絡電流\(I_s [KA]\)は次の値となる。
\[\displaystyle I_s =\fbox{10}[kA]\]
なお、実際の短絡計算では、百分率インピーダンスは、リアクタンス分だけでなく抵抗分も考慮される。



コメント