2014年 問11 電力応用 ロープトラクション式エレベータ問題 (頻出)
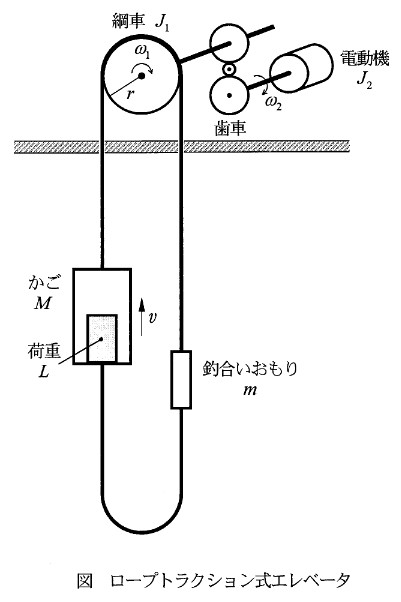
図のロープトラクション式エレベータの模式図を表している。綱車に渡されたロープの両端には、質量\(M[kg]\)のかごと、\(m[kg]\)のつり合いおもりが吊るされている。
半径\(r[m]\)の綱車には、減速比\(k\)の歯車を介して電動機が接続されている。ここで、かごに乗せる荷重を\(L[kg]\),綱車の慣性モーメント\(J_1[kg・m^2]\)、電動機の慣性モーメントを\(J_2[kg・m^2]\)とし、その他の質量、慣性モーメント、摩擦などは無視する。
1) 運転中のエレベータの速度\(v[m/s]\)とするとき、上下動するかご、荷重及び釣合いおもりの運動エネルギーの合計は、\(\fbox{ ⑥ }[J]\)となる。
このとき、綱車の回転角速度を\(\omega_1[rad/s]\)、電動機の回転角速度を\(\omega_2[rad/s]\)とすると、両者の回転における運動エネルギーの合計は\(\fbox{ ⑦ }[J]\)となる。
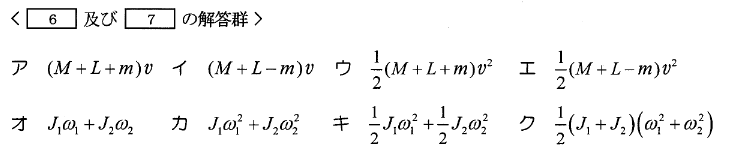
2)エレベータの速度\(v\)と綱車の回転角速度\(\omega_1\)の関係は\(v=r\omega_1\)であらわされ、一方、綱車の回転角速度\(\omega_1\)と電動機の回転角速度\(\omega_2\)の関係は、
\(\omega_1=\frac{\omega_2}{k}\)で表される。したがって、このエレベータに関するすべての運動エネルギーの合計\(E\)は\(E=\frac{1}{2}J(\omega_2)^2\)としてあらわすことができる。
ただし、\(J=\fbox { ⑧ }[kg・m^2]\)である。
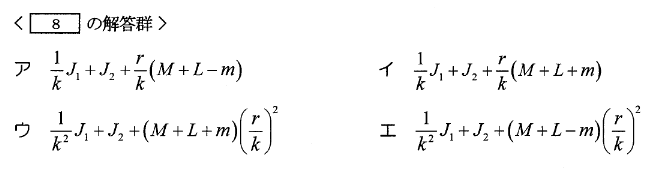
3)かごを吊り上げる方向を正として電動機の発生トルク\(T_m[N・m]\)を考えるとき、電動機軸に換算したエレベータの運動方程式は、次式で表される。
\[\displaystyle J\frac{d\omega_2}{dt}=T_m-\frac{r}{k}(M+L-m)g\]
ただし、\(g[m/s^2]\)は重力加速度とする。このとき、電動機の回転角速度\(\omega_2\)とエレベータの速度\(v\)との関係から、エレベータの加速度\(\alpha\)は\(\alpha=\fbox { ⑨ }[m/s^2]\)として求めることができる。
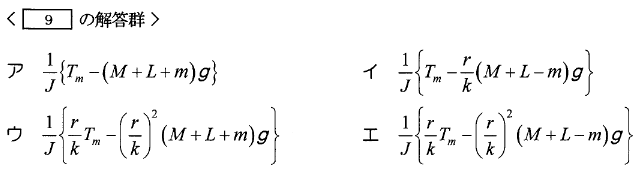
4)かごと荷重の質量合計と、釣合いおもりの質量が等しく釣り合っているとき、すなわち、\((M+L=m)\)のとき、電動機のトルク\(T_m\)とエレベータの
加速度\(\alpha\)の関係は\(T_m=\fbox { ⑩ }[N・m]\)で表される。

5)エレベータの上昇時に加速や減速させるとき、あるいは、エレベータの下降時に加速や減速させるときに、綱車には大きなトルクを必要とする。
かごと荷重の質量合計と、釣合いおもりの質量が等しく釣り合っている\((M+L=m)\)とき、必要トルクの絶対値が最大となるのは\(\fbox { ⑪ }\)するときである。





コメント