2012年 問4 自己インダクタンスと相互インダクタンス(押さえおきたい)
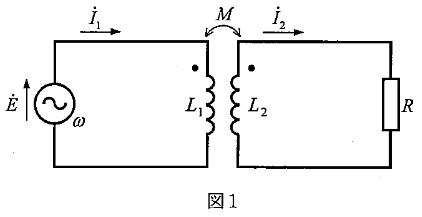
図1に示すように、電圧\(\dot{E}[V]\)と、角周波数\(\omega[rad/s^2]\)の交流電源と、自己インダクタンス\(L_1[H]\)、\(L_2[H]\)相互インダクタンス\(M[H]\)及び抵抗\(R[\Omega]\)から成る回路がある。
\(L_1[H]\)及び\(L_2[H]\)に流れる電流をそれぞれ\(\dot{I_1}[A]\)、\(\dot{I_2}[A]\)とすると
\[j \omega L_1 \dot{I_1}-\fbox{1}\times \dot{I_2}=\dot{E}・・・①\]
\[-j \omega M \dot{I_1}+\fbox{2}\times \dot{I_2}=0・・・②\]
である。①式を変形すると
\[\displaystyle \dot{I_1}=\frac{\dot{E}}{j\omega L_1}+\fbox{3}\times \dot{I_2}・・・③\]
となり、③式を②式に代入して変形すると
\[\displaystyle \dot{I_2}=\frac{M \dot{E}}{R L_1+j\omega(L_1 L_2-M^2)}・・・④\]
となる。
ここで、インダクタンスの結合係数を1とすると
\[M=\fbox{4}・・・⑤\]
の関係となることから、これを④式に代入すると
\[\displaystyle \dot{I_2}=\frac{\sqrt{L_2} \dot{E}}{\fbox{5}}・・・⑥\]
であり、電圧\(\dot{E}\)の大きさを\(E[V]\)とすると、抵抗\(R\)で消費される有効電力\(P[W]\)は
\[\displaystyle P=\frac{L_2 E^2}{\fbox{6}}・・・⑦\]
となる。





コメント