(1) ロープトラクション式エレベータを図1に示す加速度のパターンで運転する場合の走行時間や駆動力について検討する。
図1では、時間\(t = 0 [s]\) でかごが1階に停止しており、これを基準としたかごの上昇距離を
\(x [m]\)、速度を\(v=\frac{dx}{dt}[m/s]\) 、加速度を\(\alpha =\frac{dv}{dt}[m/s^2]\)とする。
また、乗り心地や安全性の観点から、加速度の範囲を\(-1[m/s^2] \leq t \leq 1[m/s^2]\)、
加速度の変化率の範囲を\(-1[m/s^3] \leq t \leq 1[m/s^3]\)に制限し、加速度を上限値及び下限値に維持する時間をそれぞれ\(T_a[s]\)、加速度を零として速度を最大値\(v_m[m/s]\)に維持する時間を\(T_b[s]\)とする。
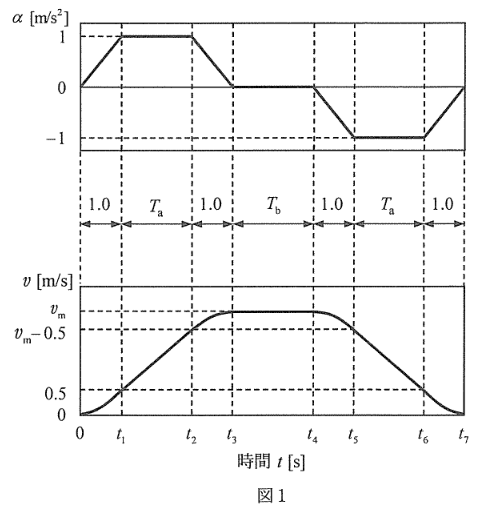
1) \(0 \leq t \leq t_3\) の期間で加速度を積分すると、\(t = t_3[s]\)での速度となることから、次式が成り立つ。
\[\displaystyle v_m =T_a+1[m/s]・・・①\]
また、停止するまでの上昇距離\(x_m\)は、\(0 \leq t \leq t_7\)の期間で速度を積分することにより、次式で求められる。
\[\displaystyle x_m =\fbox{1} \times v_m[m]・・・②\]
式①及び式②より、\(T_a\),\(T_b\) (いずれも正)により、速度及び上昇距離を調整できることがわかる。なお\(v_m\)は定格速度\(v_N[m/s]\)に制限され、上昇距離が小さい場合には、\(v_N\)以下となる場合がある。一例として 15 階建のマンションに設置されている定格速度 \(2 [m/s]\)(分速 120 m)の9人乗りエレベータを考える。移動距離が1階当たり\(3m\)とすると、1階から3階への上昇距離は\(6m\)であり、\(T_a = 1 [s]、T_b = 0 [s]\)となることから、走行時間 \(t = 4+ 2 T_a + T_b [s]\) は\( 6s\)と計算される。
同様に、1階から15階に移動する場合は、上昇距離は \(42 m\) であり、走行時間は\(\fbox{2}[s]\)と計算される。
< 1 及び 2の解答群 >
\(ア 22 \ イ 24 \ ウ 25 \ エT_a + T_b +1 \ オT_a + T_b +2 \ カT_a+ T_b + 4 \)
2) このエレベータは、最大積載質量\(600 kg\)、かごの質量が\(1000 kg\)、つり合いおもりの質量が \(1300kg\)である。乗車率を\(h (0 \leq h \leq 1)\)とすると、不平衡質量は \((600h – 300) [kg]\)、可動部全体の質量は\(\fbox{3}[kg]\)である。なお、簡略化のため、ロープの質量や走行抵抗などは無視できるものとする。
図1より、\(t_1 \leq t \leq t_2\)では加速度が \(1m/s^2\)であり、綱車から可動部に供給される駆動力\(F [N]\) を求めると、\(h=1\)の場合には \(F=\fbox{4} [kN]\) となる。また、\(t_5 \leq t \leq t_6\)では加速度が \(- 1m/s^2\) であり、\(h=0\) の場合には \(F =\fbox{5}[kN]\)となる。なお、重力の加速度を \(9.8m/s^2\)とする。
< 3 ~ 5の解答群 >
\(ア -5.30 イ -5.27 ウ -5.24 エ 5.84 オ 5.87 カ 5.90\)
\(キ (600h+2300) ケ (600h+2900) ク (600h+2600) \)




コメント