2020年問4(2)
図に示すような対称三相交流電源を持つ交流回路がある。各相の電圧を\(\dot{E_a}\)、\(\dot{E_b}\)、\(\dot{E_c}\)とし、相順は\(a→b→c\)とする。負荷は抵抗\(R=5[\Omega]\)が\(\Delta\)接続された平衡三相負荷であり、各線間電圧を\(\dot{V_{ab}}\)、\(\dot{V_{bc}}\)、\(\dot{V_{ca}}\)、線電流を\(\dot{I_a}\)、\(\dot{I_b}\)、\(\dot{I_c}\)結線の各負荷に流れる電流を\(\dot{I_{ab}}\)、\(\dot{I_{bc}}\)、\(\dot{I_{ca}}\)とする。
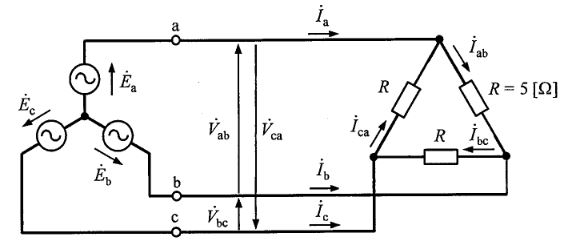
この回路において、三相交流電源から供給される有効電力を求める過程を考える。
1)三相交流電圧について考える。
\(\dot{E_a}\)、\(\dot{E_b}\)及び\(\dot{E_c}\)は対称三相電圧であるので、\(\dot{E_a}\)及び\(\dot{E_b}\)が与えられると、\(\dot{E_c}\)は定まる。
\(\dot{E_a}=100+j0[V]\)
\(\dot{E_b}=-50-j50\sqrt{3}[V]\)
\(\dot{E_c}=\fbox{7}[V]\)
線間電圧\(\dot{V_{ab}}\)は次の値となる。
\(\dot{V_{ab}}=\fbox{8}[V]\)
(2)負荷に流れる電流を求める。
電流\(\dot{I_{ab}}\)は次の値となる。
\(\dot{I_{ab}}=\fbox{9}[A]\)
電流\(\dot{I_{ca}}\)も同様に求まるので、線電流\(\dot{I_a}\)は次の値となる。
\(\dot{I_a}=\dot{I_{ab}}-\dot{I_{ca}}=\fbox{10}[A]\)
3)三相交流電源から供給される有効電力を求める。
電源の相電圧\(\dot{E_a}\)と線電流\(\dot{I_a}\)のフェザーから、力率\(\cos{\varphi}\)は\(\fbox{11}\)である。
したがって、負荷に供給される有効電力\(P\)は三相全体で次の値となる。
\(P=\fbox{12}[W]\)
2014年問4(2)
図に示すように、相電圧が\(\dot{E_a}\)、\(\dot{E_b}\)、\(\dot{E_c}\)の対称三相交流電源に、1相当たり\(\sqrt{3}+j3[\Omega]\)のインピーダンスを\(\Delta\)結線した平衡三相負荷が接続されている。ここで、相回転は\(a-b-c\)の順であり、図に示されているインピーダンス以外のインピーダンスは無視する。
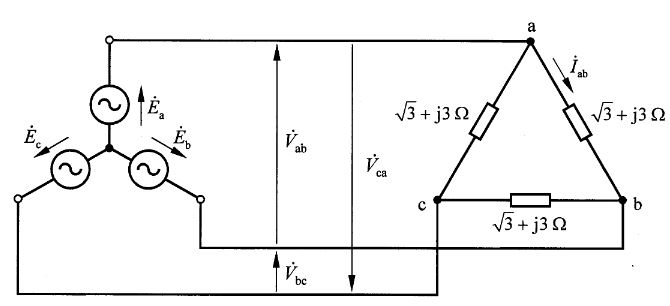
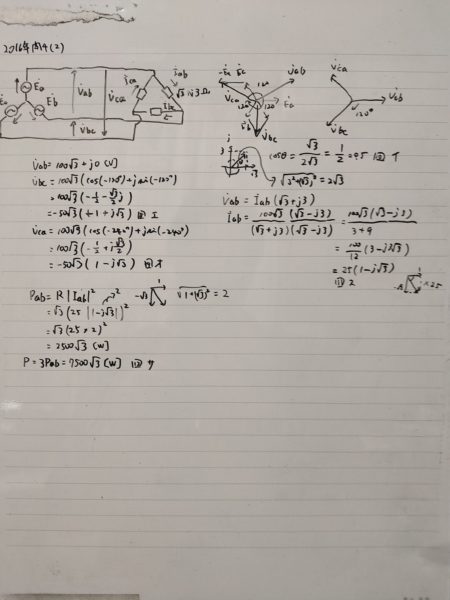
1)相電圧の大きさが\(100V\)であるとき、線間電圧\(\dot{V_{ab}}\)の位相を位相の基準とすると、各線間電圧\(\dot{V_{ab}}\)、\(\dot{V_{bc}}\)及び\(\dot{V_{ca}}\)は次のようになる。
\(\dot{V_{ab}}=100\sqrt{3}+j0[V]\)
\(\dot{V_{bc}}=\fbox{8}[V]\)
\(\dot{V_{ca}}=\fbox{9}[V]\)
2)負荷インピーダンスが\(\sqrt{3}+j3[\Omega]\)であるので、力率\(\cos \theta\)は、
\(\cos \theta=\fbox{10}\)
であり、電流\(\dot{I_a}[A]\)は次のようになる。
\(\dot{I_ab}=\fbox{11}[A]\)
また、三相負荷全体の消費電力\(P\)は次のようになる。
\(P=\fbox{12}[W]\)





コメント