電験の試験では電卓を持ち込むことができますが、その電卓の使い方がよくわからなくて、なんとなく敬遠していた。
という方に、電験の試験で良く出る計算問題をメインに電卓の重要機能であるメモリ機能を使いこなしていけるような記事になることを目指して書きました。
電卓持ち込み可。ということは、電卓を使わないと解けないような問題が出題されるからなのですが、時間の制限が厳しい電験ではこの電卓をいかに上手く使いこなすかということも一つ合格への手段になります。
自分も恐る恐る電卓のメモリ機能を使い始めましたが、すぐに慣れることができました。
今回はこの電卓を使用しています!
早速問題に慣れていきましょう。
時間短縮!電験2種で役に立つ、電卓のメモリ操作方法

まずはこちらの問題から。メモリ機能に慣れることを目的としています。
有効数字は試験と同様に3桁にします。
問0 四則演算とルートの計算
まず問題に入る前に、ルートの計算は大丈夫でしょうか。
\[\frac{\sqrt{2}}{\sqrt{3}}=?\]
この計算は。
[2][√][÷][3][√]を順番に押していきます。ルート2だからと言って、先に[√]を押してはいけません。
0.816が出てこれば正解です。
続いてメモリを使うこの問題。
$$2 \times 3+4 \times 5=26$$
電卓でそのまま左からポチポチと計算すると答えは50になってしまいます。
ですので、
[2][×][3]で出てきた答えの6を[M+]でメモリに入れます。続いてそのまま、[4][×][5]を打って出てきた20を[M+]することでメモリに元々入っていた6と追加された20を足し算してくれます。
最後に[MRC]でメモリの中の数値を呼び出せば正しく26が出てきます。
このやり方が一番スマートかなと思います。
ですが、足し算をメモリの中でしてしまうため、中身を確認することができません。
長い式を入力していると、確認したくなることもあるため、自分は次の方法で数値を確認しながら計算しました。
実際の例題で丁寧に説明していきます。
問1 インピーダンスを求める問題
\(R=6[\Omega],X=j8[\Omega]\)のとき次の\(Z\)を求めよ。
\[Z=\sqrt{R^2+X^2}\]
三平方の定理からインピーダンスを導く問題です。
暗算でもできそうなこの問題ですが、電卓を使ってゆっくり確実に解いていきます。
通常なら\(R^2\)を計算して、メモを取りながら一つずつ計算していけばいいのですが、それでは時間も手間もかかり、転記ミス、打ち間違いが多くなります。
できるだけ電卓だけで計算を完了していくためにメモリ機能を使っていきたいと思います。
まずRの二乗を計算します。
[6][×][=]の順に押すと[36]が表示される。※6×6=36と打っても大丈夫。
出てきた数字をメモリに入れるため[M+]を押す。
メモリに36が格納されました。
続いてそのまま[8][×][=]を押して64が表示される。(Xの二乗を計算しました。)
64が出ている状態で[+][MRC][=]を押す。
[MRC]を押すことでメモリに格納されていた36が呼び出されます。
すると、64+36が計算され100と表示されます。
[√]を押せば答え10にたどり着きます。
先程のスマートな手順を使うならば、
手順4,で64が表示されている状態から[M+][MRC]としても同様な答えになります。
個人的には[MRC]を押した段階で、何がメモリに格納されていたかわかる後者のやり方が好きですが、前者の使い方のほうが押すボタン数も少なくスマートです。
次の問題はそのスマートな方法で解いてみます。
その前になるべく電卓で計算する理由について書いておきます。
転記ミス、書くのに時間のかかる理由
先程問1を解く前に、転記ミス、書くのに時間がかかると書きました。
今回の問題のように\(R=6[\Omega],X=j8[\Omega]\)となっていれば問題ないのですが、\(R=0.323[\Omega],X=j0.45[\Omega]\)
となっていた場合どうでしょう。
\(R^{2}=0.104329[\Omega]\)となります。
求める答えの有効数字は電験の場合3桁なのですが、4桁だけでなく5桁目程度は誤差を大きくしていかないために計算しておいたほうが良いです。
そうなるとメモする数値は\(R^{2}=0.10433[\Omega]\)となります。
また\(X^{2}=0.2025[\Omega]\)であり、これらをメモした後に、足し算を行い、ルートを計算する。
結構めんどくさいですし時間もかかってしまいます。
だったら、全部の桁を電卓におまかせしてしまう方が楽ですし、正確です。
できる限り、メモはせずに計算機に頼ってしまいましょう。

問2 励磁回路のサセプタンスを求める問題
単相変圧器のサセプタンス \(b_0[S]\) を求めよ。ただし、
\(V=20000[V],I_0=2[A],g_0=1.5 \times 10^{-5}[S]\)とする。
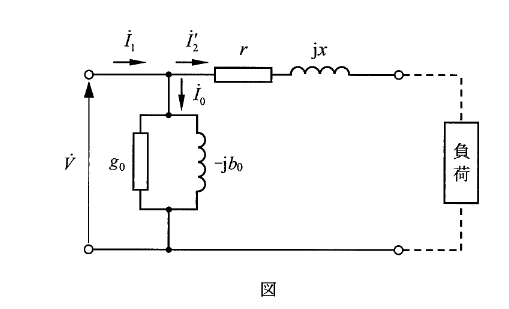
\(b_0\)を求める式は、
\[b_0=\sqrt{(\frac{I_0}{V})^2-(g_0)^2}\]
これまたややこしいですね。電験ではこういう問題が多数出てきます。
電卓で計算する場合、左から進めるのではなく、ややこしそうなところから始めるとスムーズに行きます。
今回は\(\frac{I}{V}\)のところから行きます。
マイナスの物は[M-]でメモリに格納しておき、プラスは[M+]で格納することでメモリの中で足し算引き算を計算をしてくれます。
先程の問1のやり方だと、5から手順が変わり、一つ追加されます。
この方法の利点は、
スマートなやり方はメモリ内で計算されてしまうため、ちゃんと自分がメモリした(と思っている)数字が入っているか確認ができません。
ただ、ルートの中を左から計算した結果、足し算引き算を逆にしてしまい、マイナスを消すという1手順が増えてしまっています。
お好みでいいかなと思いますが、スマートな方がおすすめです。
少しだけアクロバティックですが、慣れれば普通にできるようになります。
ここでもう一つの注目する必要があるところは、コンダクタンスである \(g_0^2\) の計算。
元々とても小さい数のため12桁の電卓でもぎりぎりです。10桁の電卓の場合エラーになってしまい、続く計算ができません。
10のべき乗は後から計算という手もありますが、ルートの中であり計算ミスを招きます。
電験2種の電卓は桁数が多ければスムーズに計算することが出来ます。
これは他の計算でも同様なケースが出てきます。

問3 解の公式の練習問題
2次方程式 \(x^2-12x+23=0\) の解の公式
\[x = \frac{-b\pm\sqrt{b^2-4ac}}{2a} \quad(a\neq 0)\]
複雑だけどよく使います。スマートな計算のやり方で解いていきます。
複雑そうなところから手を付けるため、ルートの中から計算していきます。
\[x=9.61 \quad ,\quad 2.39 \]
大分説明を省きましたが、一回もメモすること無く電卓のみで計算が完了します。
※注意点です。

問4 変圧器の効率を求める問題
変圧器効率の問題 負荷率を\(\alpha=0.8\)、変圧器出力\(P=100[kW]\)、鉄損を\(W_i=1[kW]\)、全負荷銅損を\(W_c=2[kW]\)、力率は常に1とする。
\[\eta=\frac{(\alpha)P}{(\alpha)P+W_i+(\alpha)^2W_c}\]
だんだん大変になってきましたが、メモの必要はありません。メモリ機能を使っていきます。
分母が大変そうな感じ。さらに二乗のついている\(W_c\)から計算していきます。
続いて分母第一項のPを計算します。
これで分母第一項と第三項がメモリの中で足されました。
続いてWiメモリ内で足した後でメモリから数値を引き出します。
出てきた分母を逆数にします。
Kが電卓上に表示されますが気にしない。
続けて分子をかけます。
答えは\(0.972 (97.2\%)\)となります。

問5 誘導機の一次側換算電流を求める問題
誘導機の一次側換算電流を求める問題。かなり複雑ですが、これをメモ無しでできると早いです。
\(r_1=0.1[\Omega] , r’_2=0.05[\Omega] , x_1=0.4[\Omega]\)
\( x’_2=0.3[\Omega] , E=400[V] , s=0.2 \)とする。
(Eは線間電圧、\(r’_2 , x’_2\) は一次側換算値)
\[I_1=\frac{1}{\sqrt{(r_1+\frac{r’_2}{s})^2+(x_1+x’_2)^2}}\frac{E}{\sqrt{3}}\]
さぁ、最後の問題です。
分母の\(r’_2\)が大変そう。\((r_1+\frac{r’_2}{s})^2\)から計算していきます。
次にx1,x’2周辺を計算していきます。
分母のルートを計算する。
逆数を取る。
残りの電圧をかける。
295.08・・・と出れば正解。
\[I_1=295[A]\]
お疲れさまでした。メモリの使い方はなんとなく理解できたでしょうか。
ペンを持ち替え、電卓をたたき、メモし、というのが時間的にかなりのロスになることがわかるかと思います。
慣れるとあっという間に計算できるようになります。ぜひ使いこなせるようになってください。

問6 番外編・比速度
終わりのつもりでしたが、おまけの一題です。
水車の比速度を求める問題です。
\[N_s=N_n \frac{P_T^ \frac{1}{2}}{H^ \frac{5}{4}}\]
分数の乗数が出てくるので迷う方がいると思いますのでこの部分のやり方を紹介します。
今回の場合は電卓で計算可能です。
この式の中で\(H^ \frac{5}{4}\) が引っかかるところだと思いますので、ここだけ。
\(H^ \frac{5}{4}\) は \(H^{\frac{1}{4}+\frac{4}{4}}=H^{\frac{1}{4}} \times H\) です。
ですので。
です。\(H=3\)だった場合、答えは\(3.95\)となります。
MRとMCが別々の電卓も紹介。
ここまで練習問題を解いてきて、かなり慣れてきたのではないかと思います。
ですがメモリ機能を使えば使うほど、うっかり残してしまうもの。
メモリのみクリアできる[MC]はあってもいいかな?と思うこともあります。
※ [MC]の使い方間違っていたらすみません!計算途中でも[MC]で消去できると勝手に思っています。
メモリ機能を多用する電験の強い味方になるのではないかと思います。
最後に

自分は電験2種の勉強を始めるまで電卓のメモリ機能を使ったことがありませんでした。
使ってみてかなり便利だということがわかります。
電験の2種試験は、時間との勝負になります。
その中で、一分でも一秒でも早く解ければその分見直しだとか検算だとかに時間を費やせます。
早く確実に解くためにも、試験勉強中でもなるべく計算問題は数値を入れて電卓を使用して慣れておくことを強くおすすめします。
今までほとんど使用していなかった電卓でしたが、試験が終わるころには相棒のように常に傍にいる存在になりました。
しっかり慣れていただき、試験の力強い味方になってくれることを祈っています。
それでは!






コメント
非常に参考になりました。
さっそく今日から問題を電卓で効率よく解くことができないかやってみます。